Cómo hacer un gráfico de control: Ejemplo resuelto en calidad

¿Qué hacer ante las variaciones de un proceso? ¿Cómo tomar decisiones basados en datos? El diagrama de control es la respuesta.

Creado por Walter Andrew Shewhart en 1920, el diagrama o gráfico de control, también conocido como diagrama de Shewhart, carta de control o diagrama de comportamiento de proceso, es una de las 7 herramientas de calidad definidas por Ishikawa.

Básicamente consiste en los datos de un proceso plasmados de forma cronológica en una gráfica con límites establecidos, lo que permite determinar cuándo una variación no es normal.

Es el tema de hoy para la gestión del negocio.

Qué es un gráfico de control

Una de las herramientas de análisis y solución de problemas es la gráfica de control. Es un diagrama que muestra los valores producto de la medición de una característica de calidad, ubicados en una serie cronológica. En él establecemos una línea central o valor nominal, que suele ser el objetivo del proceso o el promedio histórico, junto a uno o más límites de control, tanto superior como inferior, usados para determinar cuándo es necesario analizar una eventualidad.

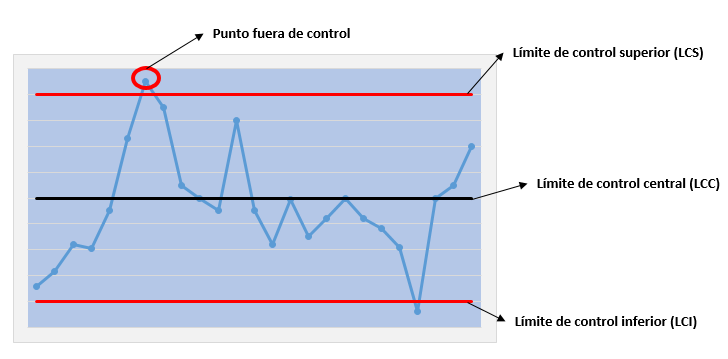
¿Qué logramos con esto?

Imagina que eres un productor de tornillos y que cada tornillo que haces debe medir entre 3,55 cm y 3,60 cm. Menos de 3,55 cm o más de 3,60 cm se consideran tornillos defectuosos. Por ende, estableces tu límite de control superior en 3,60 cm y tu límite inferior en 3,55 cm. Anotas las medidas de los tornillos que produces a diferentes horas del día. Un día ves que en el gráfico de control, hay 7 tornillos producidos a las 3 de la tarde que están por fuera de los límites, ¿qué paso ahí?

La respuesta al primer interrogante es: Adquieres control del proceso. Siguiendo el ejemplo de los tornillos, el paso siguiente es determinar porqué ocurrió esa variación en el proceso. ¿Acaso fue una causa aleatoria? ¿Quizás fue una causa asignable?

Veamos algunos términos antes de conocer qué tipos de gráficas hay.

• Causa asignable: Si consigues hallar una causa concreta o que ocasiona una variación excesiva y obedece a una situación especifica, hablamos de causa asignable. Es el tipo de causa que debemos corregir. Por ejemplo la deficiente capacitación del trabajador o la falta de ajuste de una máquina.
• Causa aleatoria: Cuando no consigues hallar una explicación concreta a una variación, o si la variación fue ocasionada por un evento sin importancia que no se volverá a repetir, hablamos de causa aleatoria. También se le suelen llamar variaciones naturales o causas naturales. Es el tipo de causa que esta presente en la vida misma, fortuita. Ejemplos son la curva de aprendizaje del trabajador y el cierre inesperado del software.
• Límite superior de control: Es el valor más grande aceptado en el proceso. En español LSC, en inglés UCL (Upper control limit).
• Limite inferior de control: El opuesto al superior, es decir, el valor más pequeño. LIC en español, LCL en inglés (Lower control limit).
• Límite central de control: Con siglas LCC, es la línea central del gráfico. Entre más cerca están los puntos a la línea, mas estable es el proceso.

Beneficios: ¿Para qué entonces un gráfico de control?

¿Para qué sirve un diagrama de control entonces?

Con lo que hemos detallado hasta el momento ya tenemos varios beneficios definidos.

• Análisis de proceso: Puede que nunca se haya hecho un control estadístico de proceso. Un análisis con gráfico de control donde estableces los límites de control, te permitirá analizar ese proceso y determinar qué es lo normal en él, cuando algo no está bien, o si ha mejorado o empeorado a través del tiempo. Un proceso analizado con esta herramienta, es un proceso controlado, que es precisamente el segundo beneficio.
• Control de proceso: Conoces el comportamiento del proceso. ¿Es estable?, ¿se mantiene? ¿qué tan frecuente se sale de control? Esto te permite intervenir sobre el proceso para mejorarlo. Este, a continuación es el tercer beneficio.
• Mejoramiento del proceso: No basta analizar y controlar un proceso. Es necesario mejorarlo. Con el diagrama de Shewhart identificamos dónde se generaron las fallas y tenemos datos de entrada para hacer análisis de causas en aras de plantear soluciones a las fallas.

Tipos de gráficos de control

La característica de calidad a medir determina el tipo de diagrama de control. Inicialmente encontramos dos clasificaciones:

Gráfica de control por variables

La característica de calidad que se mide es una variable continúa (peso, pulgadas, temperatura, etc). Si ese es el caso, podemos encontrar gráficos basados en la tendencia central () y en el rango.

• Gráfica : Qué tanto se están alejando las mediciones de la tendencia central, que en este caso es la media o promedio. Por ejemplo un nuevo trabajador o nuevos instrumentos de trabajo harán que las mediciones se alejen más de línea central.
• Gráfica R: Qué tanta ganancia o pérdida de uniformidad hay en la dispersión de un proceso dentro de una muestra. En otras palabras, el rango es la resta del valor más grande con el valor más pequeño de una muestra, lo que nos permite determinar la variabilidad. El valor resultante es plasmado en un gráfico de control para ser comparado con el rango de otra serie de muestras. Con esto logramos ver si hay presencia de uniformidad en los puntos ubicados o si no, para intervenir.
• Gráfica -R: Utilizamos ambos tipos de gráficas cuando se miden la relación de las especificaciones de calidad con la tendencia central y la dispersión. En este sentido, ubicamos una gráfica ligeramente encima de la otra y analizamos el comportamiento de cada punto.

Gráfica de control por atributos

Piensa en una característica de calidad basada en atributos como el cumplimiento con respecto a una especificación. Lo hacemos con variables discretas. De aquí se derivan cuatro tipos de gráficos:

• Gráfico p: En él medimos el porcentaje de defectos por muestra. Por ejemplo si tenemos una muestra de 100 productos y 10 de ellos tienen al menos un defecto, hay una fracción defectuosa de 0,1. Este valor se ubica en el gráfico sobre el eje y.
• Gráfico np: A diferencia de p, este valor no es una fracción. Es el número de unidades defectuosas en una muestra. Si es una muestra de 100 productos, 10 de ellos tienen al menos un defecto, 10 será el valor a ubicar en el gráfico sobre el eje y.
• Gráfico c: Es el número de defectos por unidad de producción durante un período de muestreo. En este caso, los defectos por producto se cuentan, y establecemos un valor para definir a partir de cuántos defectos una unidad es defectuosa. Por ejemplo, el número de zonas desgastadas que tenga una chaqueta de cuero, si la chaqueta tiene más de 5 zonas desgastadas, se considera una unidad no conforme.
• Gráfico u: Similar a p pero parte del gráfico c. En él medimos el porcentaje de defectos en una unidad durante un período de muestreo.

Cómo hacer un gráfico de control: Paso a paso

Hay diversidad de softwares que tienen funciones para hacer montones de cosas con cartas de control. Incluso, en empresas de producción, hay maquinarias que elaboran a medida que producen las cartas de control según la configuración asignada. Pero como este no es el caso y de lo que hablamos en Ingenio Empresa es de aprendizaje, vamos a explicar cómo hacer un gráfico de control.

Aún cuando es un paso a paso, si es importante que complementes lo aprendido aquí con otras fuentes, pues el diagrama de control y en general el control estadístico de procesos es un tema mucho más grande, que incluye distribuciones de probabilidad, fórmulas, niveles de sigma, etc.

En todo caso, el control estadístico de procesos es un tema próximo a desarrollar en detalle en Ingenio Empresa.

• Paso 1. Antes que nada, determina cuál es el proceso a trabajar y cuál es la característica de calidad que vas a medir. ¿Acaso es peso, longitud, número de defectos o volumen?
• Paso 2: Ahora que tienes el tipo de datos a recolectar, define el tipo de gráfico de control a usar basándote en lo explicado anteriormente, y no te quedes solo con eso, investiga más.
• Paso 3: Determina el tiempo en el que estarás capturando los datos y define con base en el tipo de gráfico que vas a trazar, cuestiones como la cantidad de muestras a considerar (considera al menos 20) y el tamaño de cada una.
• Paso 4: Recopila los datos.
• Paso 5: Determina la línea central y el límite de control superior e inferior.
• Paso 6: Representa los datos en la gráfica.
• Paso 7: Analiza el resultado. Interpreta el gráfico.

Interpretación de un gráfico de control

Y este apartado es únicamente para el paso 7, pues aquí radica la verdadera utilidad de una carta de control. Existen comportamientos y patrones en los datos representados, que nos darán un indicio de que hay una variabilidad no aleatoria que debe investigarse.

• Pista 1: Cuando hay solo un punto fuera de control. Es quizá la más pequeña de las probabilidades.
• Pista 2: Cuando hay dos de cada tres puntos sucesivos ubicados a un lado de la línea central y más de dos desviaciones estándar (sigma) alejados de esta línea.
• Pista 3: Cuando hay 4 de cada 5 puntos sucesivos ubicados a un lado de la línea central y más de una desviación estándar (sigma) alejados de esta línea.
• Pista 4: Cuando hay una serie de 8 puntos sucesivos ubicados a un lado de la línea central, sin importar cuántas desviaciones estándar estén alejados de la línea central. Por ejemplo 8 de cada 10 puntos, 12 de cada 14 puntos o 16 de cada 18 puntos.
• Pista 5: Cuando hay 6 puntos consecutivos ascendentes o descendientes.
• Pista 6: Cuando hay 14 o más puntos consecutivos cruzando la línea central de arriba a abajo, sin que haya al menos 2 puntos sucesivos en un mismo lado.
• Pista 7: Cualquier patrón recurrente que estés observando, puede ser considerado algo inusual.

Ejemplo de diagrama de control

Vamos a imaginar una empresa que produce escritorios, por ejemplo, Mesfir. Ellos quieren monitorear el número de defectos en sus mesas incluyendo el 99,73% (tres desviaciones estándar) de la variación aleatoria del proceso, por lo que revisan que la forma de la mesa, su estabilidad y la pintura estén en óptimas condiciones.

Paso 1: Se van a contar el número de defectos encontrados en las mesas por lote. Los lotes pueden variar levemente de tamaño, es decir, puede haber pequeñas variaciones en el número de mesas que compone un lote de producción.

Paso 2: Se van a trabajar lotes que pueden tener diferente tamaño, y se va a contar el porcentaje de defectos encontrados por lote (el lote es la muestra), razón por la cual vamos a trabajar con una gráfica de control por atributos tipo p.

Paso 3: Los datos se van a capturar durante 10 días de producción. Se van a considerar 20 muestras (20 lotes), el tamaño de cada lote lo tienes en el paso 4.

Paso 4: Estos son los datos recopilados. La fracción defectuosa es el resultado de dividir el número de errores por el tamaño del lote.

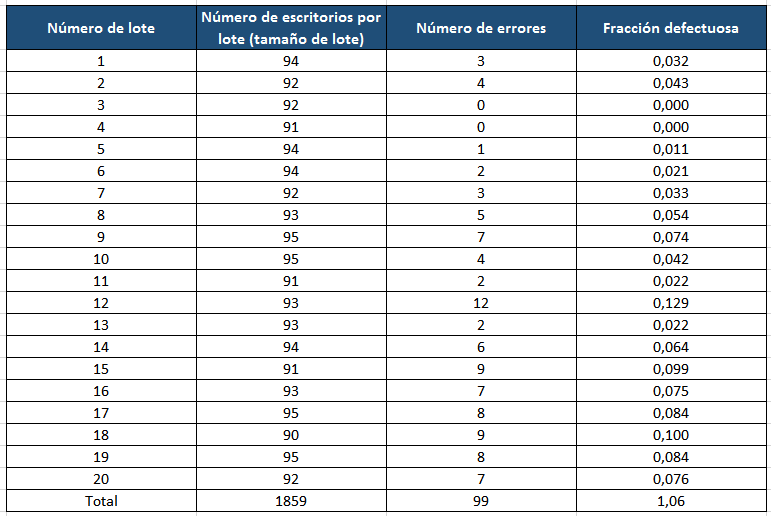
Paso 5: Vamos a determinar la línea central y los límites de control superior e inferior. Vale la pena aclarar que cuando hicimos el ejemplo, consideramos todos los decimales, sin embargo en los gráficos y fórmulas que mostramos a continuación, solo consideramos dos cifras decimales, por lo tanto seguramente si reproduces el ejemplo como se muestra a continuación, los resultados van a variar levemente.

Para tener la línea central calculamos p promedio:

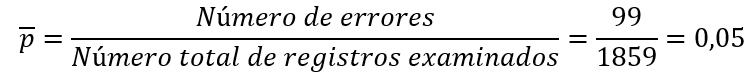
Observa la última fila del paso 4. El número de errores es 99, el número total de registros examinados es 1859 y resulta de la sumatoria del número de escritorios por lote.

La desviación estándar para la distribución de la muestra se calcula así:

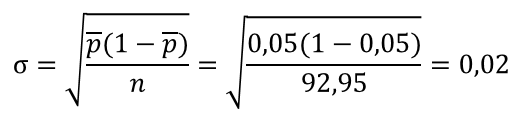
p promedio es el número que calculamos anteriormente, y n es 92,96 que es el tamaño de la muestra, en este caso el tamaño de los lotes. Como se aprecia en la tabla del paso 4, el tamaño del lote varia, por lo tanto 92,95 es el resultado del promedio de escritorios por lote. La desviación estándar es igual a 0,02.

El cálculo de los límites se hace así:

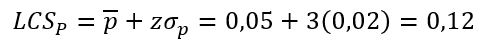
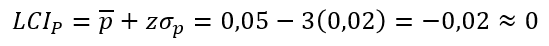
El número de desviaciones estándar se conoce como z. Mesfir (la empresa) limita los valores a 3 desviaciones estándar de la media, lo que equivale a 99,73%. Es por eso que en el cálculo de los límites de control, z es igual a 3. Los otros datos ya los conoces, fueron calculados anteriormente.

¿Podemos tener un número de defectos negativo? No. Es por eso que el límite central inferior se redondea a 0.

Paso 6: Procedemos a representar los datos en una carta de control.

Con los cálculos hechos, este es el resultado de la gráfica de control de Mesfir.

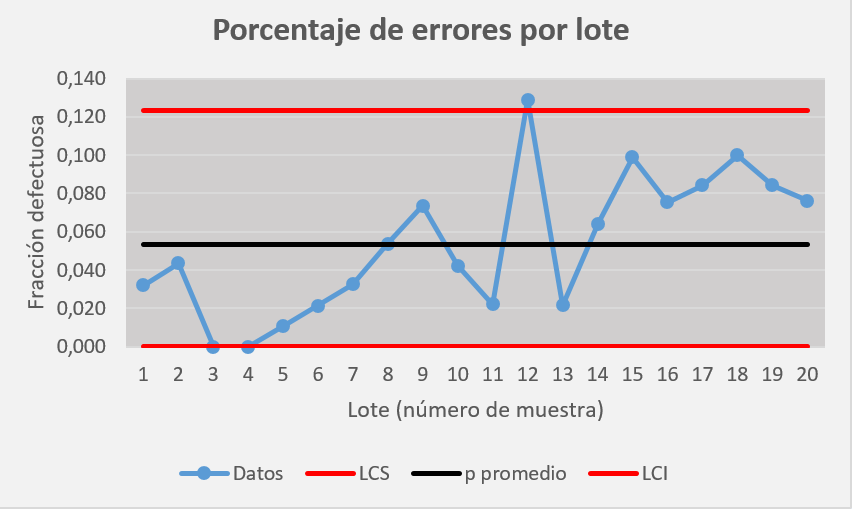
Paso 7: Analizamos el resultado.

La interpretación de una gráfica de control tiene más sentido cuando se han hecho varios ejercicios de este tipo, lo que permite determinar qué es normal y qué no lo es en el comportamiento de la producción. Sin embargo, y basándonos en las pistas antes mostradas, podemos ver que:

• El punto 12 esta fuera de control. Aunque es una probabilidad pequeña, bien vale la pena entrar a mirar porqué ocurrió esto.
• Evidentemente algo ocurrió en los lotes 4 a 9. Fija que hay un aumento constante desde el punto 4 hasta el punto 9, y aunque se ve corregido en el punto 10, se debe de revisar cómo se trabajaron estos lotes.
• ¿Qué ocurrió en los puntos 11,12 y 13? Hubo algún suceso que afectó sobre todo al punto 12 y después fue corregido; es lo más probable.

Plantilla de gráfico de control en excel

Una plantilla muy útil, tanto que me he resistido de hacer una plantilla de Ingenio Empresa por colocar esta. Es funcional, automática y dinámica. Sensacional. Esta desarrollada por la American Society for Quality (ASQ). También podrás encontrar otras plantillas en excel que te serán útiles para la gestión de tu negocio. Te recomiendo la visites.

La plantilla incluso te muestra con base en 4 criterios (pistas, comportamientos, patrones) un color diferente para aquellos puntos que se encuentran fuera de control.

• Un solo punto por fuera de los límites de control
• 2 de 3 puntos por fuera de dos desviaciones estándar (dos sigma)
• 4 de 5 puntos pro fuera de una desviación estándar (un sigma)
• 8 puntos consecutivos por un lado de la línea central

Descarga la plantilla en excel de gráfico de control

---

Derechos de imagen

La imagen destacada del post es: Designed by Freepik