Dentro de los modelos causales o asociativos encontramos el análisis de regresión o regresión lineal, que es un método con enfoque cuantitativo que nos permite pronosticar la demanda. Agrupa una variable dependiente (la demanda) con una o más variables independientes a través de una ecuación lineal.
Qué es la regresión lineal y cómo te ayudará en tu pronóstico de ventas
El objetivo del análisis de regresión como método causal es pronosticar la demanda a partir de una o más causas (variables independientes), las cuales pueden ser por ejemplo el tiempo, precios del producto o servicio, precios de la competencia, economía del país, acciones del gobierno o fomentos publicitarios.
Algunos apuntes importantes sobre éste método son:
- Puedes calcular series de tiempo y relaciones causales. En el primer caso, ubicas la demanda histórica de tu bien o servicio para que cambie en función del tiempo. El segundo caso es cuando la variable que pronosticas cambia en función de otra (variable causal).
- Lineal significa que los datos del periodo anterior y la proyección para el periodo futuro que vas a obtener caen sobre una recta.
- Si hablamos de una sola variable independiente, es una regresión lineal simple, contrario a si son dos o más variables independientes, donde hablaríamos de regresión lineal múltiple.
Cuándo utilizar la regresión lineal
El análisis de regresión es pertinente cuando se evidencia una tendencia en los datos históricos del pronóstico. ¿Cómo? Dibuja los datos de meses anteriores, los de la demanda real. Si lo estás haciendo en Excel 2010 o superior, da click derecho sobre la serie de datos graficados y luego click en agregar línea de tendencia. Si no, simplemente analiza la tendencia de los datos, ¿es creciente o decreciente?
¿Cómo es la relación entre la demanda y el tiempo? Para responder esta pregunta, haremos uso del coeficiente de correlación (r).
Este coeficiente, te permitirá entender qué tanta correlación existe entre la demanda y el tiempo.
- Correlación perfecta: Cuando el resultado de coeficiente es igual a 1 o -1. En este caso existe una relación directamente proporcional entre la demanda y el tiempo.
- Correlación fuerte: Cuando el resultado es mayor a 0.5 y menor que 1 (correlación positiva) o menor a -0.5 y mayor que -1(correlación negativa).
- Correlación débil: Valores que están entre -0.5 y 0.5.
Entre más cercano se encuentre el coeficiente de correlación a +1 o -1 más fuerte será la tendencia y más apropiado será aplicar un modelo de regresión lineal. Por ejemplo si la correlación es igual a 1, observaremos que la relación entre las variables es directamente proporcional, en el sentido que si uno aumenta, la otra también lo hará.
Bien vale aclarar que este método es más útil cuando se enfoca en periodos de largo plazo. Esto aunado a su utilidad para estimar la demanda en función de variables independientes.
Veamos entonces de que va el análisis de regresión.
El análisis de regresión en el pronóstico de demanda
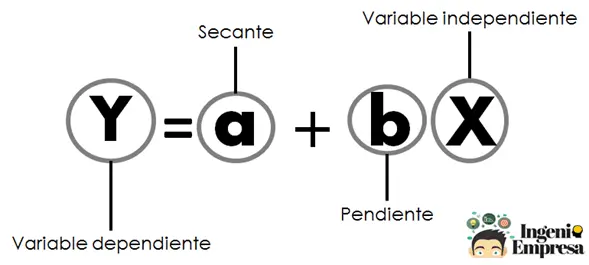
Esta es la ecuación de la recta. En ella:
- La b es la inclinación de la recta.
- La a es la secante o la altura en la que la recta corta al eje y.
- La X es nuestra variable independiente.
- La Y es nuestra variable dependiente, nuestro pronóstico calculado para un periodo.
Como hacer una regresión lineal
Un ejemplo de regresión lineal para pronosticar la demanda:
Las ventas de la empresa IngE durante los últimos 10 trimestres son las siguientes:
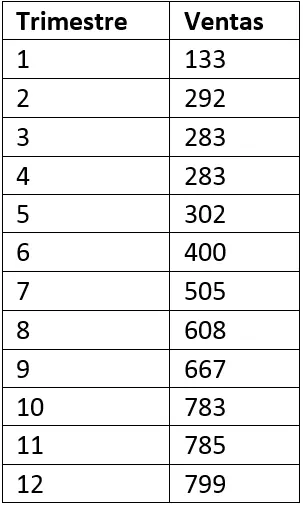
¿Cómo pronosticar la demanda de los trimestres 13, 14 y 15 a través de un análisis de regresión lineal?
Lo primero es estimar los parámetros. Lo podemos lograr con el método de mínimos cuadrados, que nos permite encontrar la recta que mejor se ajusta a un conjunto de datos dados. En nuestro caso, este conjunto está dado por las ventas trimestrales (variable dependiente). La variable independiente es el tiempo. Vamos entonces a la siguiente fórmula para determinar a y b:
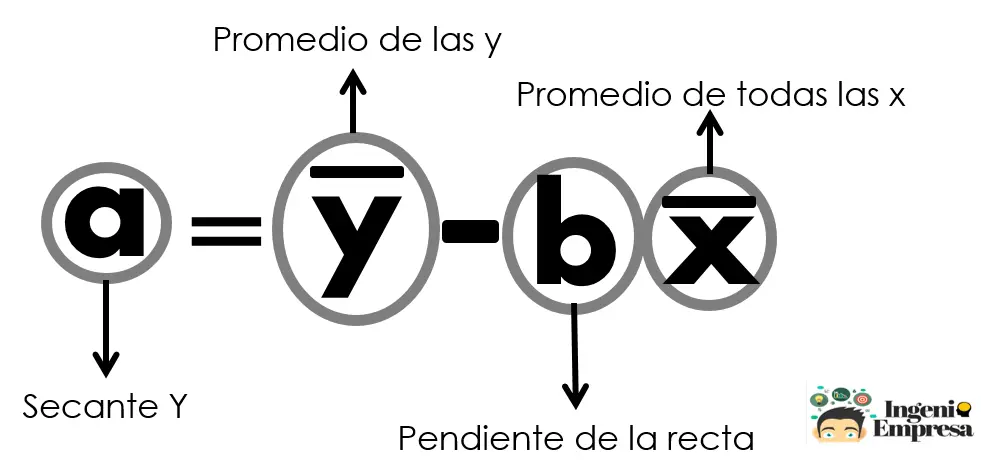
- La y “minúscula” es el valor y de cada punto de datos.
- La n es el número de punto de datos.
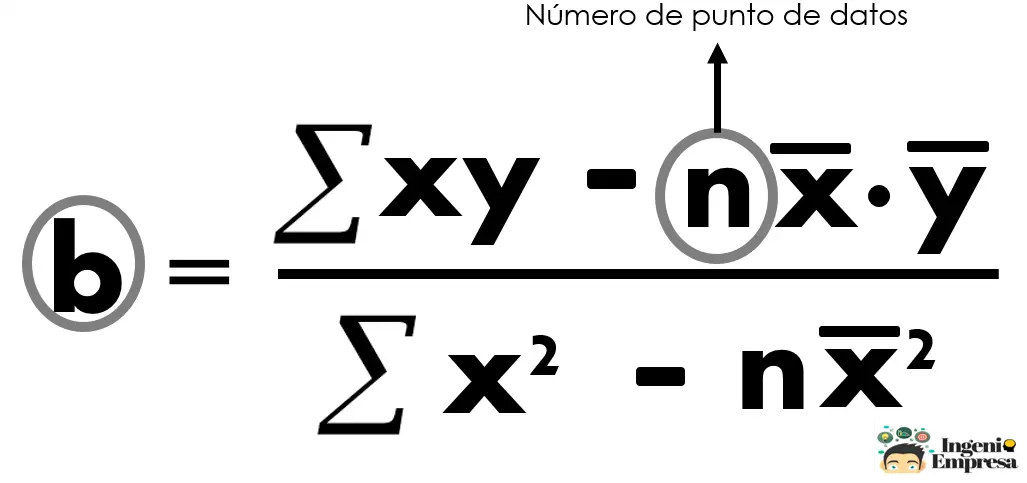
Conocidas las ecuaciones y el papel de las variables, vamos a calcular el pronóstico con regresión lineal:
En la siguiente se encuentran los cálculos realizados para los 12 trimestres según lo requerido por las ecuaciones:
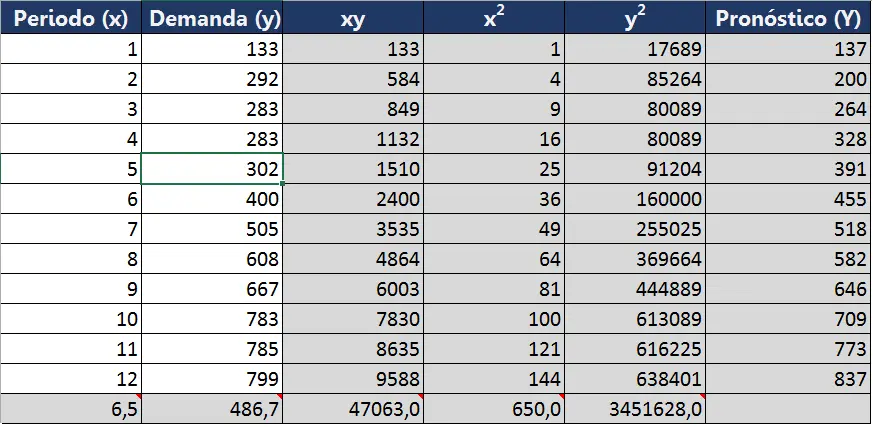
Con los valores de la última fila de la tabla, podemos calcular a y b, con los cuales logramos calcular los valores de la última columna (Y) que es la recta que más se ajusta a la demanda y.
Veamos entonces:

Fíjate que el valor de «b» varía de 63,64 a 63,657 siendo este último el resultado si se toman todos los decimales de las variables que participan en su calculo. Para tener resultados más fiables usamos el valor de «b» calculado con todos los decimales, tal como lo aprecias cuando hallamos «a». Fíjate además que pasa lo mismo con el valor calculado de «a» y el valor que se obtiene cuando en la operación están todos los decimales.
Con esta aclaración, puedes ver cómo se realiza el pronóstico de producción del trimestre 13. Procedemos igual para los demás trimestres.
Y=63,657(14)+72,894=964.09
Y=63,657(15)+72,894=1027.75
Eso tiene el siguiente aspecto:
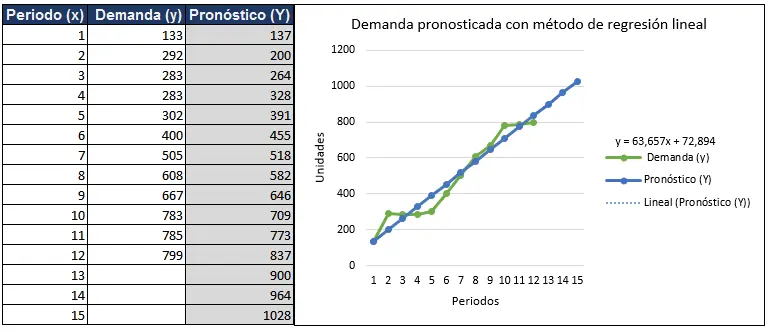
Cuando pronosticamos, siempre queremos saber qué tan exacto es el método que estamos utilizando, igual que una medida de error de pronóstico.
Para eso hay diferentes medidas que nos dan el grado de error en un pronóstico.
Una medida apropiada para medir el error en regresión lineal es el error estándar de estimación (Sy,x), que nos permite determinar la variabilidad en torno a la recta de regresión.
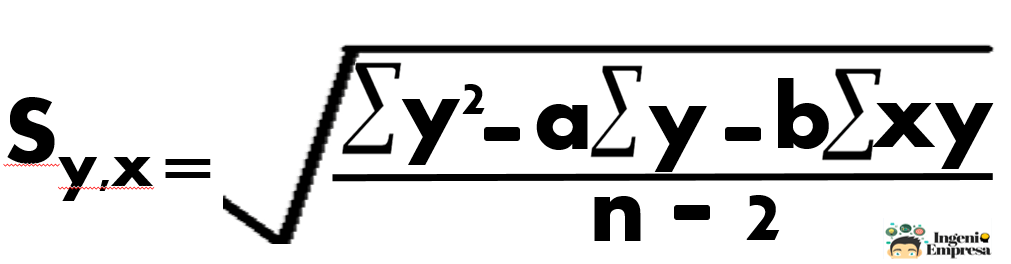
Con los datos obtenidos en nuestra tabla, reemplazamos en la formula y obtenemos:
Error estándar del estimado Sy,x: 54,79
Esto lo interpretamos como una medida de la variabilidad o dispersión de los valores observados alrededor de nuestra línea de regresión.
Otro análisis que si o si debemos realizar cuando trabajamos con un análisis de regresión, no importa si es con un fin de pronóstico, es el cálculo del coeficiente de correlación.
Como lo dijimos anteriormente, el coeficiente de correlación dará una medida de asociación entre las variables X y Y.
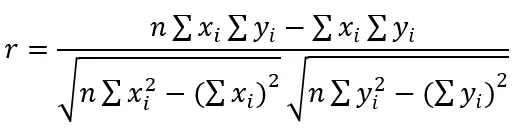
Dicho de otra forma, el coeficiente correlación en la división entre la covarianza y el producto de las desviaciones estándar de ambas variables.
Así pues, si queremos ver la correlación entre la demanda y lo pronosticado en periodos anteriores (desde el periodo 1 hasta el 12), usamos la función COEF.DE.CORREL de excel.
La función requiere dos datos de entrada:
- Matriz 1: Señalamos las demandas por mes.
- Matriz 2: Señalamos los pronósticos por mes.
El resultado de este ejercicio es r=0,975. Esto indica que la correlación es muy fuerte y positiva porque está cercana a 1.
En otras palabras, nos conviene seguir usando este método de pronóstico para futuros períodos.
Plantilla en excel regresión lineal
La siguiente es una plantilla en excel para pronosticar demanda a través del método de análisis de regresión. Escribe únicamente sobre las celdas de color blanco: el periodo (numérico) y la demanda de cada uno. Las celdas de color gris son de cálculo automático.
¿Qué tal? Esta y otras plantillas en excel las tienes en descarga directa en la sección de recursos para estudiantes.
Los comentarios han sido desactivados debido a que la mayoría lo hacían para solicitar la plantilla en excel de análisis de regresión.
En el post menciono que, los modelos y plantillas en excel se pueden descargar desde la sección recursos (en el menú superior tienes la opción). Una vez en la sección de recursos, busca plantillas en excel. Allí encontraras esta y otras plantillas en descarga directa.
pasame la tabla porfavor
Buenas noches, me podría enviar la planilla por favor
La fórmula para obtener el coeficiente de correlación está mal.
No puedo descargar la plantilla me apoyas con el archivo
Hola, me ha sido muy útil la información, no puedo descargar las plantillas, podrías enviármelas?
me podria enviar la plantilla porfavor
muy buenas tarde, ¿cual es el procedimiento para calcular el valor del pronostico de Y en la ultima columna de la tabla???
Hola buenas tardes amigo, me podrias enviar la plantilla de Excel a mi correo por favor.
No la puedo descargar, me ha sido de mucha utilidad esta pagina.
De antemano muchas gracias por tu atención.
Atte: Julio César Rodriguez
Hola como estas? como hago si mis datos de ventas no son de manera creciente si no que varian, hago la formula y el resultado que me arroja de objetivo es inferior a la venta del ultimo mes Gracias!!
Hola Leo. No pasa nada que tus datos sean de manera creciente, si bien este método puede funcionar mejor con ese comportamiento de datos, el que no sea así no es un impedimento para usarlo. Supongo que estas usando la plantilla que aquí se descarga. Si en el último mes te arrojo un resultado inferior, es porque en ese momento ese fue el pronóstico, algo inferior a lo que realmente vendiste. Con los datos que tienes pronostica nuevamente y luego anota la demanda real… si la diferencia entre lo real y lo pronosticado es mucha, considera cambiar de método.
hola buenos días, como saco el promedio de X y Y en excel.
como saco los promedios de las variables
Buena explicación. ¿Podrías enviarme la plantilla por favor? Gracias de antemano.
Gracias por la respuesta. Bueno para no complicarme mucho quisiera empezar con esto: Que el sistema me notifique cuándo debo realizar un pedido. Tengo los datos historicos de las ventas por producto (son no perecederos). Lo que estoy pensando hacer es aplicar el metodo de punto de reorden el cual me pide la demanda en el tiempo que tarda en llegar el pedido. Ahí es donde entraria el metodo de pronóstico de demanda no?, mi pregunta es cuál metodo puedo usar, me baje las 5 plantillas de excel para pronostico, saqué los errores de cada metodo pero nose cómo interpretarlos y elegir uno. Y otra cuestion es que si estaria bien que mi sistema, en base a la demanda y el pronostico, eliga el metodo adecuado, o de plano lo programo para que calcule con un metodo elegido. Talvez estas preguntas deberia hacerlas en el otro post, disculpas
Hay varias cosas que puedes hacer.
Te sugiero lo siguiente: Inicialmente toma tus datos históricos y con ellos calcula cada uno de los pronósticos. Podrías hacer un gráfico de lineas donde plasmes el comportamiento histórico de la demanda (digamos de un año) con otra serie que sea lo que te arroja el pronóstico. Hazlo con cada método y por cada mes determina el sesgo, o sea la diferencia entre lo arrojado por el pronóstico y lo que en verdad se demandó.
Con esto ya tendrás una impresión de qué métodos se adaptan al comportamiento de tu demanda. Acto seguido puedes complementar este análisis con las medidas de error de pronóstico. Te cuento un poco más de su interpretación aquí
Sobre si casarte o no con un método… tomaría la decisión después del análisis. Puede que un método funcione más en cierto período y que otro se ajuste mas para períodos posteriores, como puede que haya uno solo apropiado en el tiempo.
Excelente explicación. Gracias. Nose si me puedes hacer un favor, estoy desarrollando un sistema de ventas y quisiera implementar una seccion que haga un pronostico de abastecimientos, osea cuando y cuanto se deberia pedir por producto. Qué modelo puedo utilizar y qué datos necesito. De antemano gracias.
Hola Jesus.
Lo que mencionas me suena a un problema de inventario. Se me ocurre lo siguiente…
Si hablamos solo del «cuanto» requieres tener un registro de las ventas históricas. Con eso tendrás datos para generar pronósticos de demanda con el método más apropiado, de los cuales hablamos en Ingenio Empresa. Aquí entran otros aspectos a tener en cuenta como la vigencia del producto, por ejemplo si hablamos de alimentos pedir mensualmente podría ser un lapso de tiempo algo largo según el alimento.
Si hablamos del cuando y cuanto, además de tener en cuenta el tema anterior, debes considerar el inventario y que su costo sea el mínimo. Entiendo que conoces la demanda del inventario, por lo tanto te recomiendo buscar sobre modelos deterministicos de inventario. Aquí no hemos hablado de ello, pero en internet y libros hay bastante escrito.
Me cuentas como te va. Un saludo.
hola buenas tardes
Tu información es muy completa y muy buena. Tu me podrías colaborar enviándome la plantilla de excel?
Muchas gracias
Quedo atenta
Hola Paola. La encuentras al final del post.
Hola, me gusto mucho la información del sitio, pero no pude acceder a la plantilla me la pueden enviar porfavor 🙂
Hola Micaela. En el post coloco el enlace a la zona de descarga de plantillas de excel.
Diego muchas gracias por compartir la información me podrías mandar la plantilla.
saludos.
hola me gustaría que pudieras poner la formula ya sustituida del «error estándar de estimación» para que pueda comprender bien que valores son y como los tengo que acomodar porque no me sale la respuesta.
saludos
Hla me enviarias la plantilla porfavor?
Hola Diego, lo que quiero entender es que me expliques que valores multiplico y despejo para encontrar a «b», ya se que ahí está formula, pero no me sale, algo estoy haciendo mal en el despeje, ¿Podrías explicarme o quizás mandarme foto del despeje?
disculpa si es muy obvio pero no le entiendo siempre se me ha dificultado este tema de despejes.
Hola Omar.
Si no lo entiendes es porque quizá me ha faltado claridad para explicar el cálculo de «b». He modificado el post para hacerlo más fácil de entender. Revisa y me cuentas.
Para los trimestres 13,14 y 15 ¿De dónde salen los valores de a y b? que por cierto después cambia de 72,894 a 72,874
Hola Omar.
Los trimestres 13, 14 y 15 son los que voy a pronosticar, por lo tanto me basé en los valores a y b calculados anteriormente con los datos de los demás períodos según lo puedes ver en la formula y tabla del post; esto con el objetivo de reemplazar estos valores en la formula de ecuación de recta Y=a+bx donde a=72,894 y b=63,657 – lo que me permitirá calcular, por ejemplo el pronóstico del trimestre «13» Y=72,894+63,657(13).
Cuando cuentes con los valores reales de la demanda de los trimestres 13, 14 y 15 y desees calcular pronóstico para el trimestre 16, cambiarán los valores de «a» y «b» y los calculas de la misma forma a la explicada en el post para luego reemplazarlos sobre la formula de ecuación de recta con x=16.
Sobre el cambio de «a» que pasa de 72,894 a 72,874, error de digitación. Muchas gracias por el aviso. Ya está corregido.
Espero me haya hecho entender y si hay dudas me cuentas.
hola que tal mi buen me podrías enviar la plantilla por favor
gracias y saludos¡¡¡
Hola Jorge. En los comentarios puedes ver el enlace donde encuentras la plantilla.
Hola, me parece excelente la información pero me sería de gran ayuda si me envías la plantilla por favor.
Gracias y saludos!
La plantilla la puedes descargar haciendo una acción social en la opción que te da. Si por algún motivo no puedes, haz click aquí y buscala allí: Plantillas de excel
Entonces cual seria el pronostico de demanda para el trimestre 13?
Para el trimestre 13 sería 900,439. Tu comentario me hizo percatar de que, por razones que desconozco, el post se encontraba en una versión anterior, es decir que no estaba actualizado. En la versión que estaba no se explicaba bien el cálculo de los trimestres 13, 14 y 15, pero ya está corregido.
Te invito a verlo. Gracias Jessica.
3. Levante información histórica de volúmenes de producción, ventas o número de servicios que la empresa haya prestado en los últimos cinco años y con base en ello elabore una línea de tendencia mediante un modelo de regresión lineal y pronostique para los próximos tres años la proyección que se ajusta al modelo lineal resultante de este estudio, con su respectiva gráfica. estimado carlos es posible que me ayudes con este tema
Hola, me haría el favor de enviarme la plantilla de regresión lineal para pronosticar demanda por favor.
Hola Carlos. Si no conseguiste descargarla, también puedes intentarlo por aquí: https://www.ingenioempresa.com/tag/plantillas-en-excel/
me podria enviar la plantilla porfavor. graciass
Hola Janeth. Enviado.
Hola, me gusto mucho la información del sitio, me gustaría que me enviaran la plantilla!
No la pude descargar!
Enviado!
Estimado me envías la tabla por favor.
Enviado!
Nop ude acceder a la plantilla de regresión para el pronóstico. Me la envías?
Enviado.
hola que tal tengo una pregunta como saco n? para poder sacar mis valores a y b gracias
Hola Zuriel
El valor de «n» es el número de datos que tienes.. En el ejemplo tenemos 12 trimestres, por lo tanto n=12.
Si estuviésemos analizando las edades de 25 estudiantes, sería n=25.
n es igual al número de períodos. Saludos.