Re-cor-de-mos…
- Con los modelos determinísticos de inventario consideramos que tenemos certeza de la demanda.
- Que la demanda puede ser constante a través del tiempo o puede variar de un período a otro.
Hoy para la sección de gestión de inventarios, hablaremos de modelos determinísticos variables de inventario. Iniciamos.
¿Qué es un modelo determinístico variable de inventario?
Es el modelo bajo el cual consideramos que tenemos cierto grado de conocimiento sobre la demanda, pero esta cambia de un período a otro, o sea es variable o dinámica; por lo tanto las decisiones que se tomen frente al nivel de inventario, su reabastecimiento y el tamaño del pedido, no es algo que se pueda decidir a través de un modelo EOQ básico.
Te puede interesar: ¿Cómo saber qué tipo de demanda es la que tengo? Descúbrelo con este método.
No son pocos los modelos que han propuesto estudiosos del tema. Como te imaginarás, cada situación presenta características diferentes, por eso conviene analizarla bajo la lupa de varias técnicas de dimensionamiento de lotes para definir el que más se ajusta, y ese será el que nos dé los mejores resultados para nuestro inventario ($$$).
Hoy en Ingenio Empresa estudiaremos cada uno de ellos de forma práctica.
¡Vamos ya!
Cómo determinar el tamaño del lote
Siendo entonces que tenemos una demanda conocida pero variable (dinámica), surge la pregunta de cuánto voy a ordenar (o cuanto voy a producir) de determinado artículo, en otras palabras, ¿cuál es el tamaño del lote?
Para introducir este concepto, voy a citar un ejemplo ya mencionado en el post de planificación de requerimientos de material. La parte que está en negrilla es la que vamos a tratar en este post.
El día de hoy vienen unos invitados importantes a la casa y hoy toca lasaña. Decide entonces la cantidad de lasaña por hacer a partir del número de personas. Hacer esa lasaña involucra un procedimiento en el que se usan unos materiales e insumos específicos, como la carne, el pan y la salsa; o sea que tiene que definir cuánto necesita de cada ingrediente. Pero además, debe de conocer qué hace falta por comprar porque en el inventario ya cuenta con algunos ingredientes, pero hacen falta otros. Para apoyarse, cuenta con la receta y el conocimiento del tiempo que se demora preparando los ingredientes, haciendo el plato y su tiempo en el horno. Todo esto para que los invitados tengan su cena a tiempo y calentita en sus mesas.
Así pues, vamos a aprender cuánto pedir de cada ingrediente y en qué proporción por pedido (tamaño del lote) a fin de que el costo en la despensa (costo de inventario) sea el menor.
Para fortalecer las bases de este tema entendiendo cómo se relaciona con la planificación de la producción te recomiendo una lectura del MRP (Plan de requerimientos de material).
Tipos de modelos para tamaño de lote dinámico
Ya con todo lo dicho, solo queda contarte qué métodos nos permitirán determinar el tamaño del lote y su clasificación.
- Regla simple: De uso muy extendido por su fácil aplicación. La cantidad a ordenar se define considerando una regla de decisión. En este grupo caen la técnica de lote a lote y cantidad periódica de pedido.
- Reglas heurísticas: A diferencia de regla simple, los métodos heurísticos consideran varias reglas y procedimientos racionales. Pueden llegar a dar con la solución óptima. En este grupo está el método de Silver-Meal, costo unitario mínimo, costo total mínimo y balance de período fragmentado.
- Wagner Within: Ya hablaremos de el más abajo. Es único entre los métodos, por eso no se agrupa con otros.
Te puede interesar: Cómo realizar la valoración de un inventario
Para la decisión del tamaño del lote contamos con varios modelos determinísticos de inventario. Otros lo llaman sistemas de lote y técnicas de dimensionado de lote.
- Técnica de lote a lote
- Técnica de período constante
- Cantidad económica de pedido (EOQ)
- Cantidad periódica de pedido (POQ)
- Balance parcial de período (PPB)
- Costo Unitario Mínimo
- Método de Silver – Meal
- Algoritmo de Wagner – Whitin
Ejemplo de calculo de tamaño de lote
Arrancor es una empresa que fabrica motocicletas y se encuentra en la tarea de calcular el dimensionado de lote y el costo de inventario para el artículo espejo tipo B.
Este ejercicio se realizará las próximos 8 semanas, en las cuales y con base en los pronósticos de ventas y los pedidos anticipados de clientes, los requerimientos de producción (necesidades brutas) son los siguientes:
- 160 unidades en la semana 1
- 166 unidades en la semana 2
- 220 semana 3
- 271 semana 4
- 210 semana 5
- 188 semana 6
- 161 semana 7
- 170 semana 8
Los costos son los siguientes:
- Costo de mantener: $0,50
- Costo de ordenar: $250
- Tiempo de entrega (lead time): Una semana
La definición de los métodos puede resultar confusa si no sigues el ejemplo, por lo que te recomiendo hagas conmigo el ejercicio. Al final del post dejo el archivo en excel para que confirmes los cálculos y me alertes si, quizá ha habido un error.
Iniciamos con el método más simple de todos.
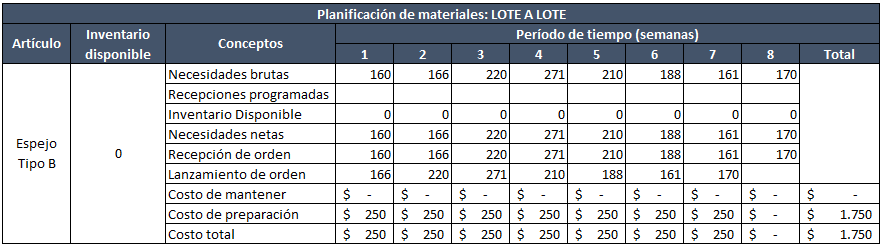
Método de lote a lote (LxL)
Si te leíste el artículo de MRP, ya sabrás en qué consiste este método. En este caso, se produce exactamente lo que se requiere, evitando que lo que se pide en un período se use más adelante en otro período. Esto conlleva a bajos costos de posesión de inventario.
Eso es lo que lo hace un ejercicio fácil. Es especialmente útil cuando contamos con un sistema de inventario justo a tiempo (JIT – Just in time).
Considerando que el lead time es de una semana, el lanzamiento de la orden de producción debe hacerse una semana antes para tener las cantidades requeridas en el momento en que sean demandadas (momento de recepción de orden).
Paso 1: En la semana 1: Las necesidades netas están dadas por la resta entre las necesidades brutas y el inventario disponible (160-0)=160. Para atender estas necesidades, debemos recepcionar un pedido por la misma cantidad, por lo tanto en recepcionar pedido colocamos 160.
Paso 2: En la semana 2 no tenemos inventario disponible ni en el resto de las semanas, pues vamos a ordenar justo lo que necesitamos. Siendo así, desde esta semana las necesidades netas serán siempre las mismas que las necesidades brutas. En este caso, 166 unidades. Recordemos que el tiempo de entrega es de una semana, por lo tanto para tener 166 unidades en recepción de orden, antes debimos hacer el lanzamiento de orden en la semana 1.
Paso 3: Repetimos el mismo procedimiento con las demás semanas.
Paso 4: Para calcular los costos de mantener, multiplicamos el inventario disponible de cada período por el costo de mantener por unidad. La bondad de la técnica lote a lote es que hace pequeño los costos de mantener, en nuestro caso de cero. Los costos de ordenar están presentes en siete semanas; 7 ordenes*$250=$1750.
Paso 5: Sumamos los costos de ordenar y mantener para obtener el costo de inventario total.
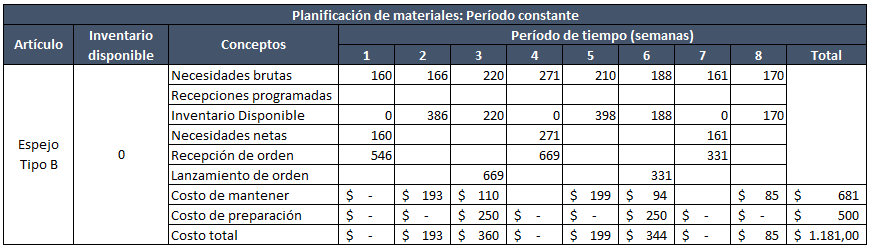
Técnica de período constante
Es muy utilizada en la industria por su sencillez. El período de reaprovisionamiento se realiza con base en la experiencia o intuición de la empresa, es decir que guarda una constancia en el tiempo (cada 4 días, cada semana, cada quince, etc).
El tamaño del lote dependerá entonces del intervalo de tiempo constante definido, lo que indica que la cantidad a ordenar deberá ser ajustada con base en la suma de los requerimientos de producción según el intervalo de tiempo considerado.
Siguiendo con el ejemplo, vamos a considerar un período de reaprovisionamiento de tres semanas. Recuerda que el lead time es de una semana.
Paso 1: Determinamos las necesidades netas de la semana 1 hallando la diferencia entre Necesidades brutas-inventario disponible (160-0)=160.
Paso 2: Sumamos las necesidades de las próximas 3 semanas para definir cuántas unidades se requieren recepcionar en la semana 1, en este caso es: (160+166+220)=546 unidades se reciben en la semana 1.
Paso 3: Hallamos el inventario disponible de la semana 2 restando el consumo de la semana 1, así (546-160)=386. Para la semana 2, tenemos unas necesidades de 166 unidades, con lo pedido en la semana 1 podemos suplirlas.
Paso 3: Nuevamente, hallamos el inventario disponible de la semana 3 igual que lo hicimos en el paso 2. El inventario disponible es igual a las necesidades brutas.
Paso 4: Procedemos igual con las semanas 4, 5 y 6. Fíjate que en el período 3 deberá hacerse el lanzamiento de la orden para que esté en el momento justo para suplir las necesidades de las semanas venideras, esto teniendo en cuenta que el lead time es de una semana.
Paso 5: Calculamos el costo total de la misma forma que lo hicimos con el método anterior.
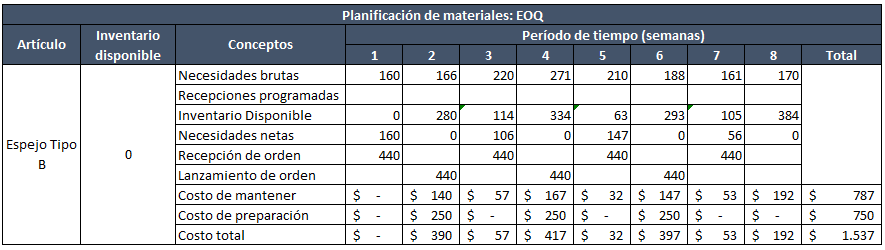
Cantidad económica de pedido (EOQ)
Es el mismo modelo EOQ del que hablamos antes. Recordemos que con el EOQ determinas el tamaño de lote (cantidad económica de pedido) haciendo coincidir el costos de mantenimiento y colocación de pedidos.
Con la cantidad que arroje el modelo EOQ podremos determinar los períodos de reaprovisionamiento de inventario.
Es preferible usar el lote económico cuando se conoce la demanda (esto debido a que se trata de artículos de demanda independiente, es decir que están condicionados a la adquisición de otro artículo) y no tanto con demanda constante.
¿Cómo procedemos?
La formula del EOQ que ya mencionamos en un post anterior menciona que debemos tener la demanda anual. Podemos hacer un estimado de la demanda anual si calculamos la demanda promedio del horizonte de planificación y lo multiplicamos por el número de períodos en un año.
En nuestro caso, el horizonte de planificación es de 8 semanas y tenemos 52 semanas en un año.
Veamos:

Aclaración: Hemos calculado el EOQ de dos maneras distintas. En la primera, calculamos D anual hallando la demanda promedio (193,28) y multiplicando por 52 que son las semanas del año. Luego al calcular el EOQ, como se toma la demanda anual, también multiplicamos H por 52. En la segunda forma, se calcula D hallando el valor de la demanda promedio (este es un D del período de planificación y no D anual), mismo valor que se coloca en la formula de EOQ.
El resultado del MRP lo tienes aquí:
Cantidad periódica de pedido (POQ)
Este método es una combinación del EOQ y del método período constante. Partimos con la cantidad óptima de pedido (Q*), este valor nos permitirá hallar la cantidad de pedidos (f) y luego cada cuánto se debe lanzar el pedido (T*).
Por lo tanto, las unidades de T* deberán satisfacer la demanda de los próximos períodos.
Teniendo entonces el valor EOQ visto en el método anterior:
Aclaración: La frecuencia de pedido f la hemos calculado de dos maneras distintas. En la primera consideramos la demanda anual (10059) dividida sobre el EOQ, y luego dividida por el número de semanas del año, el resultado luego se multiplica por 8. La otra forma es dividir la demanda de unidades del périodo de planificación sobre el EOQ. Ambos resultados arrojan 3,51 que es el número de pedidos que se generan durante el horizonte MRP.
Por lo tanto, ordenamos para 2,27 períodos, o sea para 2 períodos.
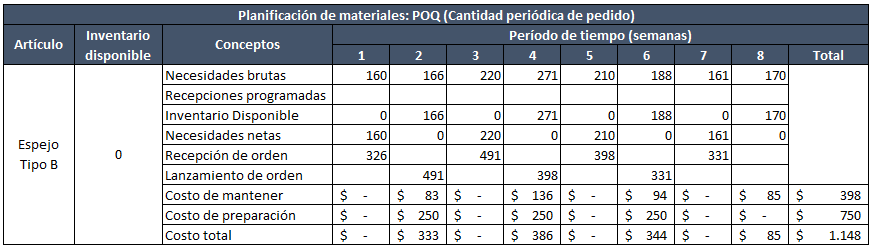
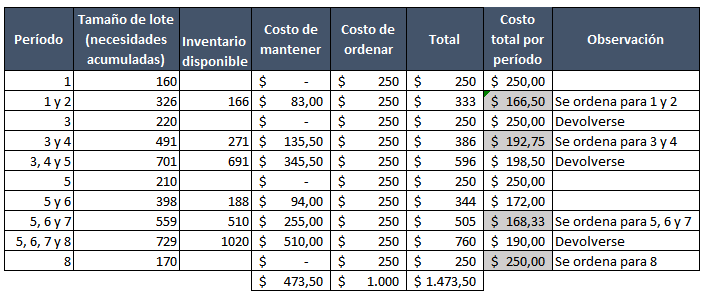
Balance parcial de período (PPB) o Costo total mínimo
También conocido como costo total mínimo. Al igual que el EOQ, el balance parcial de período o balanceo de período fragmentado busca el equilibrio entre el costo de mantenimiento y colocación de pedidos considerando el siguiente lote del futuro.
El método consiste en pedir para la necesidad actual y las necesidades futuras, tantos períodos sean que se consiga hacer la diferencia entre el costo de mantener y ordenar la menor posible.
Recordemos entonces que nuestro costo de ordenar es de $0,5. El de ordenar es $250 e iniciamos con la primer semana:
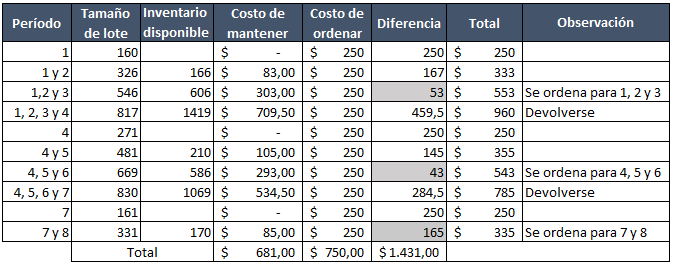
Paso 1: Partimos con una orden para una sola semana. El tamaño de la orden será de 160 y como se consumirá en ese mismo período, no hay costo de mantener, por lo que la diferencia con el costo de ordenar |250-0|=250.
Paso 2: Ahora consideramos una orden para la primer y segunda semana. El tamaño será entonces de 326 (160+166). El inventario será de un período a otro será de 166, mantenido por un (1) período nos ofrece un costo de mantener de 166*0,5=$83,0 … eso nos otorga una diferencia entre el costo de ordenar y mantener de |250-83|=167. ¿Nos entregará un lote para la semana 1,2 y 3 una diferencia menor? Veamos.
Paso 3: Agregamos otra semana. El tamaño será de 546 (160+166+220). El inventario será de (166+2(220))=606 unidades, que mantenerlas nos genera un costo de 606*0,5=$303,0. La diferencia entre el costo de ordenar y mantener es igual a |250-303|=53. La diferencia disminuyó, fue menor que la definida en el paso 2, ¿será menor si agregamos otra semana?
Aclaración: Fíjate que para determinar las unidades en inventario consideramos el número de semanas que duran las unidades requeridas por período. Recordando que en paso 3 consideramos primer, segunda y tercer semana: Las de la semana 1 (160) se consumen de inmediato y por eso no generan costo de mantener; las de la segunda semana (166) duran una semana en inventario; las de la tercer semana (220) duran 2 semanas en inventario, por ende se multiplica por 2 cuando hallamos las unidades de inventario.
Paso 4: Mismo procedimiento. Tamaño del lote es igual a (160+166+220+271)=817. El inventario es igual a (166+2(220)+3(271))=1419 unidades. Este valor multiplicado por el costo de mantener una unidad nos da 1419*0,5=709,5 que es el costo de mantener ese lote. La diferencia con el costo de ordenar es |250-709,5|=459,5. La diferencia aumentó con respecto a la calculada en el paso 3, nos indica devolvernos y pedir para la semana 1, 2 y 3.
Paso 5: A partir de la semana 4, repetimos el mismo procedimiento.
El resultado, lo tienes a continuación:
Fíjate que se ordena para los períodos 1, 2 y 3; 4, 5 y 6; 7 y 8. Esto debido a que la diferencia entre el costo de ordenar y mantener fue menor que en los casos anteriores y siguientes.
Con los tamaños de lote, elaboramos el MRP tal como ya lo hemos hecho con los métodos MRP anteriores.
Fíjate que el costo total de inventario al calcular el tamaño del lote ($1431) no coincide con el de la planificación MRP ($1181). Esto es así porque al decidir sobre el tamaño del lote, sumamos el costo de ordenar para la semana 1. En cambio en el MRP para la semana 1 no consideramos costo de ordenar, pues tenemos un lead time de una semana, lo que ubica el costo de ordenar a los períodos anteriores fuera de nuestra planificación.
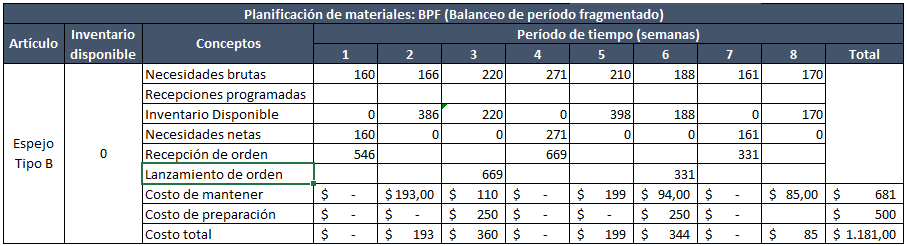
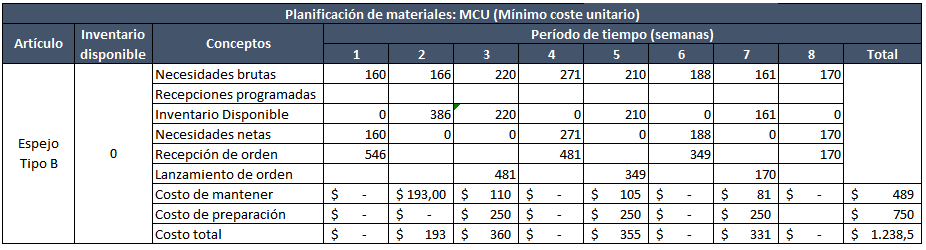
Mínimo coste unitario (MCU)
Similar a Silver – Meal y BPF. Se considera el costo variable promedio por unidad para definir la cantidad a ordenar. Decimos promedio porque en este método sumamos los costos de mantener y ordenar para luego dividirlo por el tamaño de cada lote para elegir el que presente un menor coste unitario.
Esto con el objetivo de encontrar el período de reaprovisionamiento que minimice el costo total unitario.
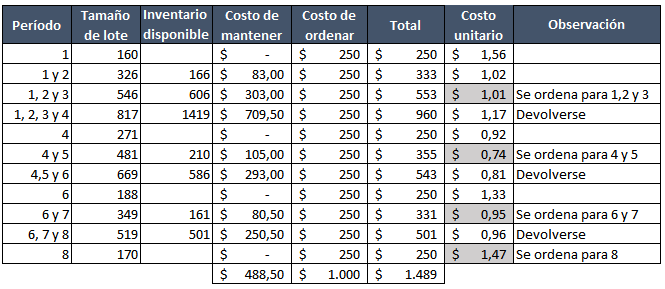
Paso 1: Si pedimos para una sola semana, no habrá inventario disponible porque se consumirá esa misma semana, lo que significa que no habrá costo de mantener pero sí costo de ordenar. Entonces, él costo total de inventario es la suma del costo de ordenar más costo de mantener es: 0+250=$250. El costo unitario promedio estará dado por la división del costo total entre el tamaño de lote: $250/160=$1,56. Agregamos otra semana para ver si nos da un costo unitario menor.
Paso 2: El tamaño del lote es de 326 unidades. El inventario en ese hozizonte es de 166*1=166, que significa que las 166 unidades del período 1 están en inventario durante una semana. Ese valor multiplicado por el costo de mantener es 166*0,50=$83,00. El costo total de inventario es 83,00+250=$333. El costo unitario lo obtenemos diviendo el costo total de inventario sobre el tamaño del lote: 333/326=$1,02. Es menor que el hallado en el paso 1.
Paso 3: Repetimos los calculos. Tamaño de lote es de 546 unidades. El inventario es (166*1)+(2*220)=606 unidades. El costo de mantener es 606*0,50=$303. El costo de inventario es 303+250=$553. Por último, el costo unitario es 1,01. Es menor que el del paso 2, por lo que agregamos otra semana para ver si es menor que el obtenido en este paso.
Paso 4: Haciendo los calculos para un tamaño de lote de 817 unidades (semana 1 a la 4), obtenemos un costo promedio unitario de 1,17. Siendo mayor que el costo unitario obtenido en el paso 3, nos devolvemos y pedimos para la semana 1 a la 3.
Paso 5: Repetimos el procedimiento.
El MRP con MCU es el siguiente:
El costo total de inventario del MRP no coincide con el de la decisión de tamaño de lote debido a que en la semana 1 del MRP no se incluyó el costo de preparación.
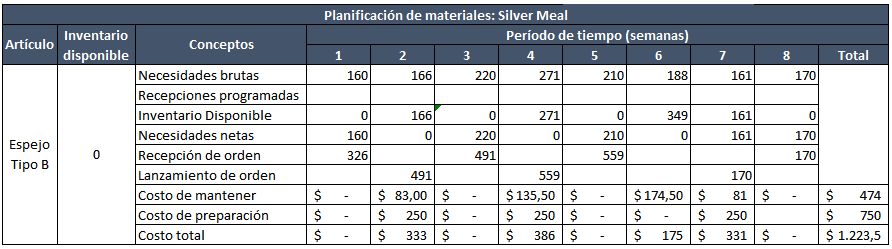
Algoritmo Silver – Meal
Considera el costo promedio del período (costo de ordenar y costo de mantener) para definir la cantidad a ordenar (o reaprovisionamiento), cantidad pensada para varios períodos futuros.
Dicho de otra forma, con este método se determina el costo promedio mínimo por período según la cantidad de períodos a futuro generados por el pedido.
Su procedimiento es similar a BPF y MCU, solo que esta vez el criterio de decisión es el costo total por período.
Es decir, una vez que tengamos el costo total de inventario (tal como lo hemos calculado en los dos métodos anteriores), debemos dividir este valor sobre el número de períodos para los que se piensa ordenar.
El ejemplo de MRP con Silver Meal es el siguiente:
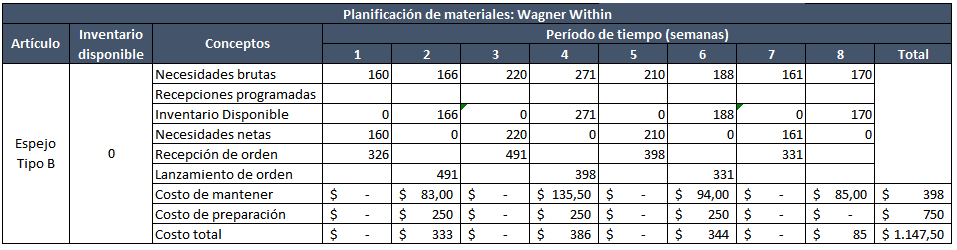
Algoritmo de Wagner – Within
A través de programación dinámica, esta técnica busca minizar los costos de ordenar y mantener inventario a través de la evaluación de múltiples formas que logren cubrir la demanda de cada período. Este ejercicio resulta en la determinación de la cantidad óptima de pedido que minimiza el costo de inventario.
Su aplicación es un poco más compleja al involucrar programación dinámica, pero su uso ha comenzado a extenderse en software MRP. Siendo así, te remito a este artículo de gestión de operaciones donde explican el método con un ejempo detallado.
En próximos post veremos con más detalle la programación para ejercicios de inventario.
Por lo pronto, este es el resultado del MRP con el algoritmo de Wagner – Within.
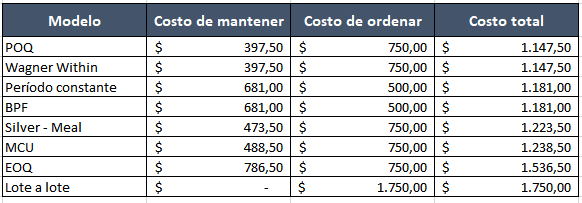
Resultado final: El mejor método es…
Nuestro ejemplo ha sido resuelto con cada uno de los ejemplos. El resultado final demuestra que el modelo determinístico variable de inventario que ofrece menor costo es…
Cantidad periódica de pedido y Wagner Within. De hecho fijate que el MRP de ambos coincide por casualidad.
Los resultados de los demás métodos están bastante ajustados, a excepción de lote a lote y EOQ que van más alla de los $1500. Con vista en la tabla, desde el POQ hasta el MCU se pueden considerar buenos resultados, pues la diferencia entre los costos de inventario de uno y otro es de tan solo |1447,5-1238,5|=$91.
Archivo en excel
Puedes revisar los cálculos descargando el archivo en excel que contiene el ejemplo resuelto. Haz click aquí para descargarlo.
Fuente
Heizer, J., & Render, B. (2008). Dirección de la producción y de operaciones: Decisiones tácticas (8 ed.). Madrid: Pearson Educación.
Sipper, D., & Bulfin, R. (1998). Planeación y control de la producción (1 ed.). México, D.F: Mc Graw Hill.

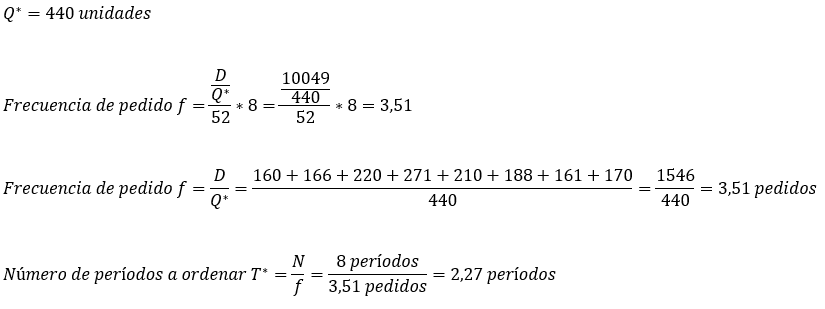
Excelente aporte, como siempre.
Tengo una duda: por mi parte trabajo en el almacén de uniformes para alrededor de 3000 personas. Estos uniformes son camisas, pantalones, overoles, etc., y vienen en diferentes tallas. Pregunto, ¿debo hacer el cálculo de loteo para cada parte (pantalon, camisa…,) del uniforme y para cada talla (s, m, L…,)?
Por último, he venido empleando el método EOQ con descuentos y la demanda la he pronosticado pues esta no es constante ni mucho menos conocida. Pero leyendo la serie de post que tiene en esta página, veo que dices que el método EOQ no es el mejor si la demanda es variable.
Quedaría muy agradecido si me pudiese sacar de estas dudas.
Y nuevamente gracias por los grandes aportes que nos brindas a nosotros lo ingenieros a través de esta página; excelente enseñanza.
Buenas muy interesante como podría hacer si demanda la calculo en años ya que en el ejemplo esta en semanas?
Debes llevar esa demanda a semanas. Por lo general se consideran 52 semanas, por lo tanto no es más que hacer la división. Recuerda también hacer la conversión para los otros datos que tengas en formato anual.
Esto es un curso completo sobre el tamaño del lote de los métodos determinístimos variables, que aprovechare para mi complemento de este de tema de Gestión de Inventarios. Les agradezco mucho.
Hola Enrique. Me alegra mucho que te haya gustado.
En el mes de junio estaremos hablando de modelos probabilísticos de inventario de revisión periódica.
Saludos!
Saludos,
Me gustaría saber si hay alguna forma de calcular los costos de mantener en inventario y pedir, puesto que en todos los modelos para determinar el tamaño de lote se requiere esta información.
Tal vez tienes alguna publicación sobre el tema.
Gracias de antemano.
Buenos días, excelente post, está explicado de una manera muy clara. Quería consultar si tienen algún post sobre como obtener el costo de mantenimiento.
En la técnica de periodo constante el costo total es de $1181, al igual que en el balance parcial de período (PPB) o Costo total mínimo, pero sólo porque la intuición de hacer el periodo constante de 3 semanas fue acertada, sino normalmente debería ser menor el costo total en el PPC, es así?
Desde ya muchas gracias.
En el punto 4 del PPB hubo un pequeño error, que no afecta al cálculo, en la diferencia con el costo de ordenar (debe decir 250-709,5). Saludos!
Hola Erick.
No por el momento, pero ahora que lo mencionas, si que sería interesante dada la importancia de este concepto dentro de los temas que estan y los que vienen en 2018.
Es correcto, el resultado del PPB y período constante fue igual por pura casualidad.
Tienes razón, error de transcripción. Está corregido. Gracias por la notificación.
Me alegra que te haya gustado el post, un saludo.